Conheça um pouco sobre umas das 17 Equações que Mudaram o Mundo!

Durante nossos anos de estudo, aprendemos diversas fórmulas matemáticas, físicas e químicas. Ao optarmos por um curso de exatas na universidade, sabemos que vamos estudar boa parte dessas fórmulas novamente – e ainda mais complexas. Mas estes conhecimentos não são importantes apenas para os estudantes e profissionais de áreas como a Engenharia, a Física e a Matemática, ao contrário do que muitos pensam – há até gifs virais nas redes sociais, como: “Passou mais um dia e eu não usei o Teorema de Pitágoras”.

E com o objetivo de divulgar a importância de diferentes equações, Ian Stewart, matemático inglês e professor emérito da Universidade de Warwick, no Reino Unido, publicou um livro em que reúne as fórmulas matemáticas que considera serem as mais importantes da história.

Em “17 Equations That Changed The World” (17 equações que mudaram o mundo), Stewart analisa desde o Teorema de Pitágoras à Lei da Gravidade, e nos mostra que a matemática e suas fórmulas estão muito mais relacionadas à história humana e a seu desenvolvimento do que um dia imaginamos.

  

Conheça um pouco mais sobre cada uma das equações:

+ Teorema de Pitágoras

Uma das fórmulas mais estudadas no colégio, e uma das maiores descobertas no campo da Matemática. Esta equação objetiva descrever a relação geométrica entre os lados de um triângulo retângulo (com um ângulo reto, de 90º, o triângulo retângulo é formado por dois catetos, dois lados que formam o ângulo reto, e a hipotenusa, lado oposto ao ângulo reto).

O Teorema de Pitágoras foi importante para o estudo dos números irracionais da Matemática, e é uma equação que diferencia a geometria euclidiana da geometria curva (este Teorema não é utilizado para cálculos de triângulos desenhados sobre uma esfera, por exemplo).

A descoberta da equação é creditada ao matemático grego Pitágoras, em 530 a.C, mas há argumentos de que a fórmula já existia, e de que matemáticos babilônicos conheciam método semelhante de cálculo.

Logaritmos

O segundo exemplo de equações fundamentais por Stewart são os logaritmos, que representam o oposto das funções exponenciais. A fórmula em evidência neste artigo, log(xy)= log(x) + log(y), é um dos exemplos clássicos de equação, que transforma a multiplicação em adição.

O estudo dos logaritmos é importante em cálculos da Engenharia, da Física e da Astronomia. Antes do avanço tecnológico e da possibilidade de realizar cálculos através dos computadores, os logaritmos possibilitavam a multiplicação de grandes números de uma forma mais fácil e rápida.

 

Derivada de uma função

O objetivo desta equação (neste caso, o quociente de Newton) é calcular a taxa de variação de um determinado parâmetro. Por exemplo, o cálculo da velocidade de corpos em movimento, a taxa de crescimento de uma população são exemplos de uma função que varia. A derivada é, portanto, necessária para a medição destas alterações, e fundamental para a Ciência.

Lei da Gravidade

A Lei da Gravidade de Newton, ou a Lei da Gravitação Universal, descreve a força da gravidade entre dois objetos, e a equação demonstra esta relação de acordo com a massa e a distância entre o centro de cada objeto.

Os estudos de Newton foram baseados em trabalhos anteriores de cientistas como Robert Hooke e Kepler, e apresentados em fins do século XVII. As conclusões de Newton eram de que a ação da gravidade acontecia da mesma maneira em qualquer parte do universo, no Planeta Terra ou no Sistema Solar, e de que quanto maior a massa do objeto, maior a força que o atrai para baixo. Anos depois, a teoria de Newton seria redefinida pela Teoria Geral da Relatividade de Einstein.

Números Complexos

Muito utilizados na Física, na Engenharia e no campo da Eletrônica, os números complexos são representados pela letra “i”. Estão inseridos nos números complexos todos os outros conjuntos numéricos.

Nas operações em que os números complexos estão envolvidos, é necessário compreender processos aritméticos, trigonométricos e algébricos. A partir destes conjuntos numéricos, é possível encontrar uma solução para quaisquer equações (que nem sempre terão uma solução em números reais).

 

Relação de Euler

A fórmula criada pelo matemático Leonhard Euler, V – A + F = 2 é a fórmula dos poliedros, em que subtraindo o número de vértices pelo de arestas, e somando ao número de faces, independentemente do formato do poliedro, o resultado será o número 2.

Entre os poliedros, o cubo é o mais conhecido, mas outros exemplos são as pirâmides e até a bola de futebol (neste caso, um icosaedro truncado). Os estudos, as propriedades da geometria sólida e a fórmula de Euler foram fundamentais para a topologia e para a física moderna.

 

Distribuição Normal

A mais tradicional da área da Estatística, a curva da distribuição normal é utilizada em diferentes áreas: da biologia às ciências sociais. Também conhecida como Distribuição de  Gauss, é um gráfico em curva utilizado para definir, por exemplo, o comportamento de grandes grupos sociais, como a distribuição de uma população.

 

Equação da Onda

Esta é uma equação diferencial, referente à propagação das ondas sonoras, luminosas ou aquáticas. Seu estudo e utilização são importantes para descrever como uma propriedade muda ao longo do tempo. A Equação da Onda é importante principalmente em áreas como Acústica e Eletromagnetismo.

 

Transformada de Fourier

Também relacionada ao comportamento das ondas, é essencial para entender processos mais complexos de propagação de ondas, como o da fala humana.O objetivo é transformar um sistema complexo em uma combinação de números de ondas simples, o que facilita a análise.

Equações de Navier-Stokes

Também exemplos de equações diferenciais, estas têm a aplicação destinada à descrição do deslocamento dos fluidos. Os estudos dos matemáticos Claude-Louis Navier e George Gabriel Stokes permitiram a simulação por computadores com relação ao deslocamento dos fluidos – líquidos e gasosos – e têm grande importância no estudo de diferentes fenômenos pela Ciência, Física e Engenharia.

 

Equações de Maxwell

Estas são equações que descrevem a relação entre eletricidade e magnetismo e têm grande importância para este campo de estudo. As Equações de Maxwell são fundamentais para o entendimento de como o eletromagnetismo funciona em nosso dia a dia.

 

Segunda Lei da Termodinâmica

Importante na criação de máquinas térmicas e utilização na indústria, versa sobre a irreversibilidade de um sistema isolado termodinamicamente, que tende a incrementar-se com o tempo, até alcançar um valor máximo. A irreversibilidade é exemplificada: ao adicionarmos um cubo de gelo em uma xícara de café, este cubo de gelo irá derreter, mas o processo nunca ocorrerá no sentido inverso, ou seja, o congelamento do café.

 

Teoria Geral da Relatividade de Einstein

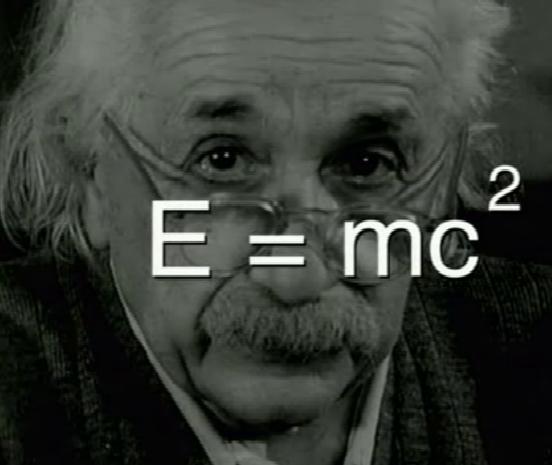Já falamos sobre a Teoria de Newton, e de como houve um desenvolvimento dos estudos sobre a gravidade a partir da Teoria Geral da Relatividade de Einstein, já no início do século XX. De acordo com o físico alemão, espaço, tempo, massa e gravidade estão intimamente ligados.

Seus estudos levaram à famosa fórmula E=mc², que mostra como matéria e energia são equivalentes, e também sobre a relatividade do tempo (que pode passar mais rápido para algumas pessoas, e mais devagar para outras). Uma das atribuições práticas das conclusões de Einstein está relacionado à calibragem dos satélites do GPS.

 

Equação de Schrodinger

Utilizada na Mecânica Quântica, avalia o comportamento de átomos e de pequenas partículas de sistemas moleculares, atômicos e subatômicos.

Os estudos e a equação de Schrodinger, físico austríaco, são importantes em áreas como a energia nuclear e na implantação de sistemas da mais alta tecnologia.

 

Teoria da Informação

Também conhecida como Teoria Matemática da Comunicação, é o cálculo do conteúdo informativo de uma mensagem, com avaliação de qual é a compressão máxima possível de um arquivo sem que haja perdas de dados. A avaliação, neste caso, não é semântica, mas sim quantitativa (em níveis de bits).

Formulada por Claude Shannon, conhecido como “o pai da teoria da informação”, é uma das mais representativas teorias, principalmente nos tempos modernos. É a teoria matemática aplicada de forma a refletirmos sobre a maneira com que nos comunicamos atualmente.

 

Teoria do Caos

Esta equação envolve a ideia de tempo e consequência. De acordo com a Teoria do Caos, uma pequena mudança no início de um processo terá grandes influências e consequências no futuro. Um dos exemplos mais significativos desta teoria é de que o simples bater de asas de uma borboleta pode causar um furacão em outro continente – o chamado efeito borboleta.

A Teoria do Caos está relacionada a diversos e diferentes fenômenos que guiam a nossa vida: dos batimentos cardíacos à Meteorologia.

Fórmula de Black-Scholes

Uma equação que define que algo é implicitamente precificado se a ação é negociada. O objetivo da Fórmula de Black-Scoles é permitir que os profissionais do mercado financeiro calculem o valor de certos produtos, como os derivativos financeiros. É um dos modelos mais utilizados no mercado.

Referência: Business Insider, Brasil Escola, Universidade de Warwick, Faculdade de Ciências da Unesp, Giz Modo, Mundo Estranho, Público

Fonte: http://blogdaengenharia.com/17-equacoes-que-mudaram-o-mundo/
Conheça o livro completo: http://goo.gl/DNIYIw